Comenzaremos con un poquito de teoría
La circunferencia es una línea curva, cerrada y plana donde todos los puntos están a la misma distancia del centro. Es importante no confundirla con el círculo, ya que este es la región del plano delimitado por una circunferencia y que posee área definida.
Aunque ambos conceptos están relacionados, no debe confundirse la circunferencia (línea curva) con el círculo (superficie).
En una circunferencia podemos encontrar diferentes elementos asociados a ella, que nos ayudarán a comprender mejor los ejercicios posteriores:
- Segmento: recta comprendida entre dos puntos.
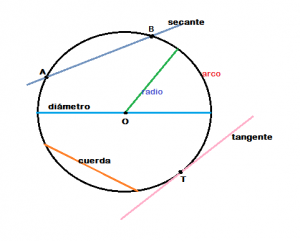
- Radio: segmento que une el centro con cualquier punto de la circunferencia.
- Cuerda: segmento que une dos puntos cualquiera de la circunferencia.
- Diámetro: linea recta que une dos puntos de una circunferencia pasando por el centro. Su longitud corresponde a la de dos radios.
- Tangente: linea recta que toca a la circunferencia en un solo punto. Este punto se denomina punto de tangencia.
- Secante: linea recta que pasa por la circunferencia atravesándola por dos puntos.
- Arco: porción de la circunferencia determinada por dos puntos.
Teniendo claro estos conceptos podremos entender mejor los de circunferencia inscrita y circunscrita:
La circunferencia circunscrita es la que pasa por todos los vértices de un polígono y contiene completamente en su interior a dicha figura.
La circunferencia inscrita es aquella que, siendo interior, es tangente a todos sus lados.
Después de este pequeño repaso, estamos listos para realizar el Ejercicio 1: Dado un triángulo, construir la circunferencia inscrita y circunscrita
1.1.- Circunferencia circunscrita a un triángulo.
1.2.- Circunferencia inscrita a un triángulo

No hay comentarios:
Publicar un comentario